addier.bar

Feiertagsmathematik
Es wäre nicht Weihnachten 2020, wenn nicht zahlreiche Dekorationen durch Klopapierrollen inspiriert würden. Immerhin lassen sich die Rollen zu stabilen, weihnachtsbaumähnlichen Pyramiden stapeln.
Vorher sollte aber berechnet werden, wie viele Rollen dafür gehamstert werden müssen… Doch wie geht das? Wen diese Frage umtreibt, dem kann mit der Gaußschen Summenformel unkompliziert geholfen werden, und die Feiertage sind gerettet.
Was gibt es schließlich Besinnlicheres, als unter dem Weihnachtsbaum über mathematische Formeln zu diskutieren? Keiner soll behaupten, Mathematik wäre alltagsfremd. Oder feiertagsfremd.
Manche kennen die Anekdote, wie der kleine Carl Friedrich Gauß im Jahr 1786 seinen Mathematiklehrer verblüffte: Anstatt alle Zahlen von 1 bis 100 schrittweise zusammenzuzählen, erkannte er, dass er jeweils 101 erhält, wenn er die erste und die letzte Zahl addiert (1+100), die zweite und die vorletzte Zahl (2+99), die dritte und die drittletzte Zahl (3+98) und dass es insgesamt 50 solcher Paare gibt. Die Gesamtsumme beträgt also 50×101=5050.
Außerdem gibt es noch die Gaußsche Osterformel, aber die ist ja momentan nicht so passend. Über 200 Jahre später schaffte Gauß es mit all diesen Formeln auf den 10-Euro-Schein.
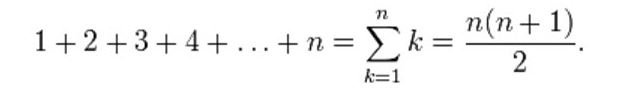
Konkret bedeutet n(n+1)/2:

Da 6 plus 1 gleich 7 ist, 5 plus 2 ebenso und 4 plus 3 auch, kann man einfach 6 mit 6 + 1 multiplizieren und das Ergebnis 42 durch 2 teilen. Es werden also 21 Klopapierrollen benötigt.

Allerdings löst bei vielen Menschen schon der Anblick des Summenzeichens mit dem griechischen Namen Sigma Beklemmungen aus. Sigma wirkt tatsächlich, als könne es jederzeit zubeißen:

Vielleicht hilft es, das Summenzeichen aus Lebkuchenteig zu backen, um es selbst anzubeißen? Wenn der Lebkuchenteig nicht ausreicht, kann das Rezept mit einem einfachen Dreisatz umgerechnet werden… aber das ist dann eine ganz andere Geschichte.
Ein Kommentar zu “addier.bar”